Задача #1
Имеем: g = 1,6 м/c²; T = 4,9 c. Найти: L - ?
1. Формула периода математического маятника:  .
.
2. Выразим длину:  .
.
3. Численно получим:  (м).
(м).
Ответ: 0,97 м.
======================
Задача #2
Дано: C =  Ф; T = 0,001 c. Найти: L - ?
Ф; T = 0,001 c. Найти: L - ?
1. Формула Томсона:  .
.
2. Индуктивность из (1):  .
.
3. Численно получим:  (Гн).
(Гн).
4. Перевод: 0,0051 Гн = 5,1 мГн.
Ответ: 5,1 мГн.
======================
Задача #3
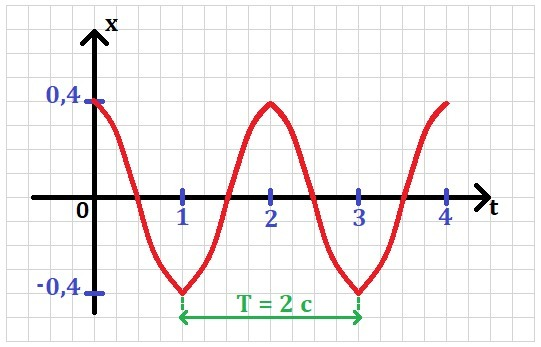
Имеем: x = 0,4cos(πt). Найти: A, T - ? Построить: x(t).
1. Уравнение гармонических колебаний в общем виде:  , отсюда амплитуда A = 0,4 м и циклическая частота ω = π рад/с.
, отсюда амплитуда A = 0,4 м и циклическая частота ω = π рад/с.
2. Формула циклической частоты:  , значит период:
, значит период:  .
.
3. Численно:  (c).
(c).
Ответ: 0,4 м; 2 с.
График зависимости x(t) смотри в приложении.