1) BM= √(AM^2-AB^2) =√(26^2-24^2) =√(2*50)=10
BC= √(AC^2-AB^2) =√(40^2-24^2) =√(16*64)=32
MC=BC-BM =32-10 =22
2) KM= √(MR^2-KR^2) =√(10^2-8^2) =√(2*18)=6
KL=KR=8
ML=KL-KM =8-6=2
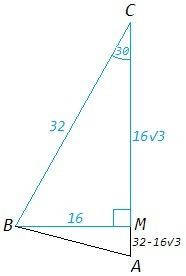
3) △СBM с углами 30, 60, 90, стороны относятся как 1:√3:2
CM=16√3, BC=32
∠ABC=180-∠A-∠C =180-75-30=75
∠A=∠ABC=75, △ACB - равнобедренный, AC=BC=32
AM=AC-CM =32-16√3
△ABM, по теореме Пифагора
AB=√(AM^2+BM^2) =
=√((32-16√3)^2 +16^2) =16√((2-√3)^2 +1) =32√(2-√3)
Или по теореме косинусов, cos30=√3/2
AB^2 =AC^2 +BC^2 -2AC*BC*cosC = 2*32^2(1 -√3/2) <=>
AB= 32√(2-√3) ~16,56