Ответ:
Smbn = 16 ед².
Объяснение:
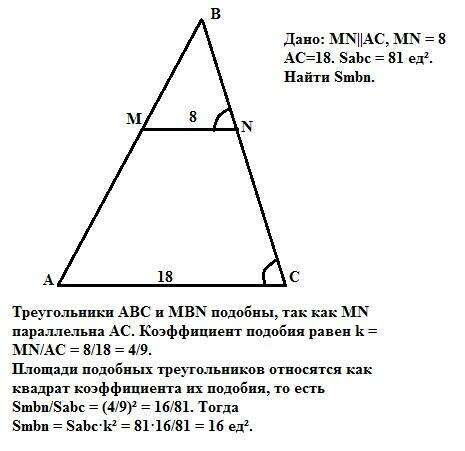
Треугольники АВС и МBN подобны по двум углам, так как MN параллельна АС и ∠А = ∠М, как соответственные при параллельных прямых, а ∠В - общий. Тогда коэффициент подобия равен
k = MN/AC = 8/18 = 4/9.
Площади подобных треугольников относятся как квадрат коэффициента их подобия, то есть Smbn/Sabc = k² =(4/9)² =16/81. Тогда
Smbn = Sabc·k² = 81·16/81 = 16 ед².