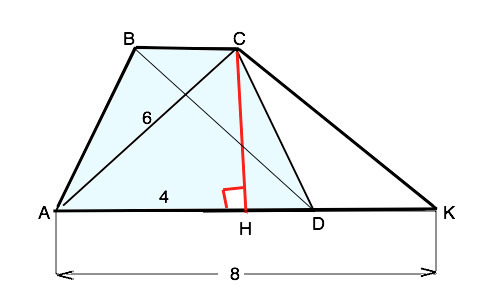
Обозначим трапецию АВСD, высоту, опущенную из вершины С - СН.
. Площадь трапеции равна произведению высоты на полусумму оснований. Полусумма оснований=средняя линия трапеции.
Способ 1) Вспомним, что в равнобедренной трапеции высота, проведенная из тупого угла к основанию, делит его на отрезки. больший из которых равен полусумме оснований, меньший - их полуразности.⇒ АН=4. ⇒ S(ABCD)=CH•AH.Треугольник АСН - прямоугольный. По т.Пифагора СН=√(AC²-AH²)=√(6²-4²)=2√5 ⇒ S(ABCD)=2√5•4=8√5 (ед площади).
Или
Способ 2). Проведем из вершины С параллельно диагонали ВD прямую до пересечения с продолжением АD в точке К. Четырехугольник DBCK- параллелограмм (противолежащие стороны параллельны), DK=BC и АК=ВС+AD=2•4=8(т.к. равно двум полусуммам оснований). Тогда площадь треугольника равна АСК равна площади трапеции, её можно вычислить по ф.Герона и получить тот же результат.