Здравствуй!
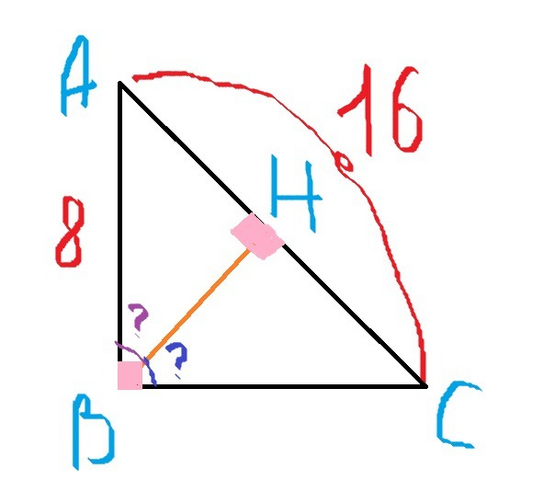
Дано: ΔАВС - прямоугольный, ∠В=90°, АВ=8 см, АС=16 см, ВH - высота.
Найти: углы, которые образует высота ВН с катетами треугольника.
Решение:
По условию АВ=8 см, АС=16 см ⇒ АВ=1/2АС ⇒ если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30° ⇒ ∠С=30°.
Так как ВH - высота, то углы ∠AHB=∠CHB=90°.
∠А=90°-30°=60°, т.к. в прямоугольном треугольнике сумма острых углов равна 90°.
Рассмотрим ΔАВH: ∠H=90°, ∠А=60°, ∠В=90°-60°=30°.
Рассмотрим ΔСВH: ∠H=90°, ∠C=30°, ∠В=90°-30°=60°.
Ответ: ∠ABH=30°, ∠CBH=60°.
Удачи в учебе!