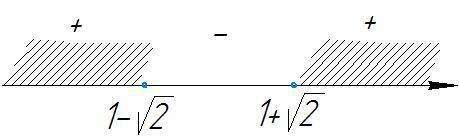Ответ:
( -∞ ; 1 - √2 ) ∪ ( 1 + √2 ; ∞ )
Пошаговое объяснение:
0\\ D=4+4=8\ ; \sqrt{D}=2\sqrt{2}\\x_{1}=\frac{2+2\sqrt{2} }{2}=1+\sqrt{2}\\x_{2}=\frac{2-2\sqrt{2} }{2}=1-\sqrt{2}\\" alt="x^2-2x-1 > 0\\ D=4+4=8\ ; \sqrt{D}=2\sqrt{2}\\x_{1}=\frac{2+2\sqrt{2} }{2}=1+\sqrt{2}\\x_{2}=\frac{2-2\sqrt{2} }{2}=1-\sqrt{2}\\" align="absmiddle" class="latex-formula">
Стандартный вид, крайний правый промежуток имеет знак " + ", затем идет чередование " - " , " + ".
Промежутки, удовлетворяющие неравенству:
( -∞ ; 1 - √2 ) ∪ ( 1 + √2 ; ∞ ).
