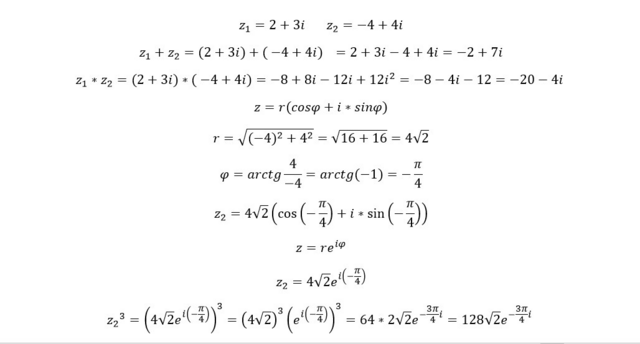Ответ:
Пошаговое объяснение:
z_1=2+3i z_2=-4+4i
z_1+z_2=(2+3i)+( -4+4i) =2+3i-4+4i=-2+7i
z_1*z_2=(2+3i)*( -4+4i)=-8+8i-12i+12i^2=-8-4i-12=-20-4i
z=r(cosφ+i*sinφ)
r=√((-4)^2+4^2 )=√(16+16)=4√2
φ=arctg 4/(-4)=arctg(-1)=-π/4
z_2=4√2 (cos(-π/4)+i*sin(-π/4) )
z=re^iφ
z_2=4√2 e^i(-π/4)
〖z_2〗^3=(4√2 e^i(-π/4) )^3=(4√2)^3 (e^i(-π/4) )^3=64*2√2 e^(-3π/4 i)=128√2 e^(-3π/4 i)