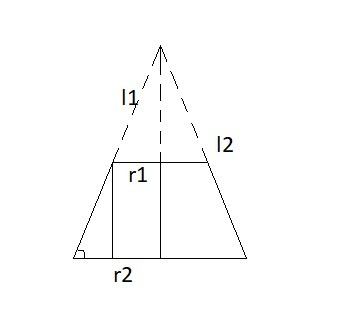
Если обозначим радиусы оснований через  (меньшее) и
(меньшее) и  (большее), а образующую усеченной части конуса через
(большее), а образующую усеченной части конуса через  и образующую большего конуса через
и образующую большего конуса через  , то площадь боковой поверхности усеченного конуса найдется по формуле:
, то площадь боковой поверхности усеченного конуса найдется по формуле:

Из прямоугольных треугольников выразим каждую из образующих через радиус основания и угол наклона образующей:

Подставим и получим: