ГЕОМЕТРИЯ 9 КЛАСС! ДАЮ 50 БАЛЛОВ! ПОМОГИТЕ, ПОЖАЛУЙСТА! 1) Даны треугольники ABC и KMN, в...

Question

ГЕОМЕТРИЯ 9 КЛАСС! ДАЮ 50 БАЛЛОВ! ПОМОГИТЕ, ПОЖАЛУЙСТА! 1) Даны треугольники ABC и KMN, в которых AB/KN = BC/MN = AC/MК. Назовите угол треугольника KMN, равный углу С. Почему эти углы равны? 2) В треугольниках ABC и KMN, в которых AB/KN = BC/MN = k. Какое равенство необходимо добавить к условию, чтобы можно было доказать подобие этих треугольников? Назовите возможные варианты

Answer 1

1)

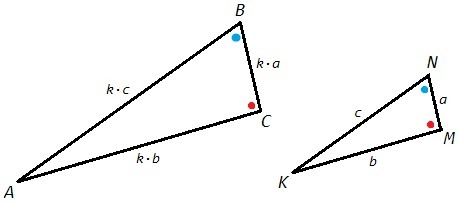
Три стороны треугольника ABC пропорциональны трем сторонам треугольника KNM, следовательно треугольники подобны.

AB/KN=BC/NM=AC/KM => △ABC~△KNM (по трем пропорциональным сторонам)

В подобных треугольниках против пропорциональных сторон лежат равные углы.

△ABC~△KNM => ∠A=∠K, ∠B=∠N, ∠C=∠M

Вершины подобных многоугольников следует перечислять соответственно равенству углов.

2)

a) Треугольники ABC и KNM подобны по трем пропорциональным сторонам:

AB/KN=BC/NM=AC/KM=k => △ABC~△KNM

б) Треугольники ABC и KNM подобны по двум пропорциональным сторонам и углу между ними:

AB/KN=BC/NM, ∠B=∠N => △ABC~△KNM

---