На стороне PQ треугольника PQR взята точка N, а на стороне PR

Ответ:

$\frac{n}{m}$

Объяснение:

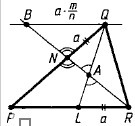
Пусть QL и NR пересекаются в одной точке - A.

NQ=LR=a

Через точку Q проведём прямую, которая параллельна PR. Пусть эта прямая будет пересекаться с прямой NR в точке B. Из подобия треугольников BAQ и RAL следует, что $BQ=LR*\frac{AQ}{AL} =a*\frac{m}{n}$

Из этого подобия треугольников BNQ и RNP находим, что $\frac{PN}{PR} =\frac{NQ}{BQ}=\frac{a}{a*\frac{m}{n} } =\frac{n}{m}$

** стороне PQ треугольника PQR взята точка N, а ** стороне PR – точка L, причем NQ = LR....

стороне PQ треугольника PQR взята точка N, а стороне PR – точка L, причем NQ = LR....