Ответ: 408 бусен
В волшебном лесу есть 30 полянок:
1)могут быть полянки без тропинок.
2) нет тупиковых полянок
3) расположение полянок неизвестно
4) тропинки не пересекаются
Вывод: от каждой "неодиночной" полянки отходят минимум 2 тропинки.
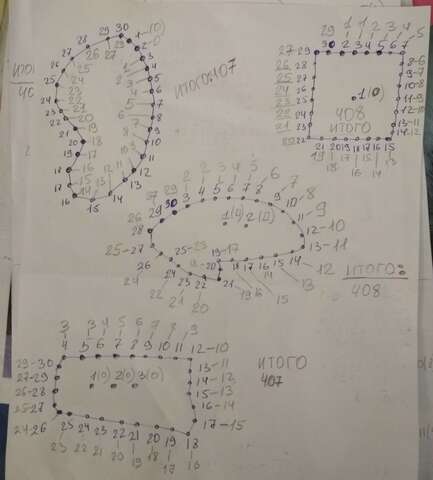
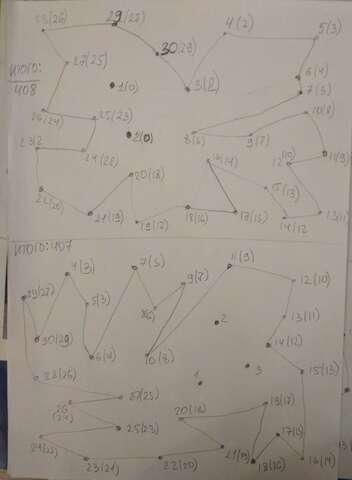
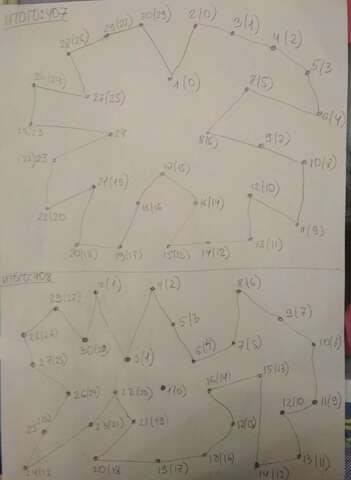
Самый затратный вариант (по вопросам), когда полянки соединены последовательно (замкнутой цепочкой) и есть несколько полянок без тропинок (смотри фото). Т.е. самый затратный вариант, когда от каждой "неодиночной" поляки отходят только 2 тропинки(но есть ещё и несколько полянок без тропинок). Если хотя бы от 1 полянки отойдёт 3 или больше тропинкок, то количество вопросов уменьшится.
У меня получился самый затратный вариант, где 1 или 2 полянки без тропинок. И там и там будет 408 вопросов (смотри фото).
Примечание: вопросы задаются с 30 полянки. Количество вопросов написано карандашом возле номера полянки (или в скобках).
Например: рассмотрим вариант, где все полянки соединены последовательно друг за другом (нет одиночных полянок)
1) на 30 полянке - 29 вопросов (про 30 поляну не спрашивал)
-------узнаем пути 30---1 и 30---29
2) на 29 полянке - 27 вопросов (про 30,29 и 1 не спрашивал)
-------узнаем путь 30---28 (через 29)
3) на 28 полянке - 26 вопросов (про 30,29,28 и 1 не спрашивал)
-------узнаем путь 30---27 (через 29,28)
2) на 27 полянке - 25 вопросов (про 30,29,28,27 и 1 не спрашивал)
-------узнаем путь 30---26 (через 29,28,27)
2) на 26 полянке - 24 вопроса (про 30,29,28,27,27 и 1 не спрашивал)
-------узнаем путь 30---25 (через 29,28,27,26)
-------------------и так далее--------------
28) на 3 полянке - 1 вопрос (про 30-3 и 1 не спрашивал)
-------узнаем путь 30---2 (через 29,28.....3)
29) на 2 полянке вопросов нет, т.к. Вася может добраться до первой полянке, через 30 полянку.
30) на 1 полянке нет вопросов, т.к.Вася знает пути на все полянки
Итого:407 вопросов
Рассмотрим вариант, где все полянки соединены последовательно друг за другом и одна 1 полянка одиночная (не имеет тропинок)
1) на 30 полянке - 29 вопросов (про 30 поляну не спрашивал)
-------узнаем пути 30---2 и 30---29
2) на 29 полянке - 27 вопросов (про 30,29 и 2 не спрашивал)
-------узнаем путь 30---28 (через 29)
3) на 28 полянке - 26 вопросов (про 30,29,28 и 2 не спрашивал)
-------узнаем путь 30---27 (через 29,28)
2) на 27 полянке - 25 вопросов (про 30,29,28,27 и 2 не спрашивал)
-------узнаем путь 30---26 (через 29,28,27)
2) на 26 полянке - 24 вопроса (про 30,29,28,27,27 и 2 не спрашивал)
-------узнаем путь 30---25 (через 29,28,27,26)
-------------------и так далее--------------
28) на 3 полянке - 1 вопрос (про 30-3 и 2 не спрашивал)
-------узнаем, что путь 30---1 ( через 29,28....3) не существует
29) на 2 полянке 1 вопрос (про 1 полянка), т.к. Вася не знает как добраться до первой полянке
------- узнаем, что путь 30---1 (через 2 полянку) не существует
30) на 1 полянке нет вопросов, т.к.Вася знает, что остальные полянки с ней не соединены.
Итого:408 вопросов задаст Вася
Ответ: 408 бусен отдаст Вася строке, если
1) 29 полянок соединены последовательно друг за другом и 1 полянка одиночная
2) 28 полянок соединены последовательно друг за другом и 2 полянки одиночные