СРОЧЬНО, 30 БАЛОВ Площа діагонального перерізу правильної чотирикутної призми дорівнює 8...

Question

32 просмотров

СРОЧЬНО, 30 БАЛОВ Площа діагонального перерізу правильної чотирикутної призми дорівнює 8 см2. Обчисліть площу бічної поверхні даної призми. Площадь диагонального сечения правильной четырехугольной призмы равна 8 см2. Вычислите площадь боковой поверхности данной призмы.

Геометрия Olar13Б_zn (256 баллов) 26 Май, 20 | 32 просмотров

Дан 1 ответ

vaskovskie91_zn · Answer 1 · 2020-05-26T05:14:16+0000

Добрый день!

Решение:

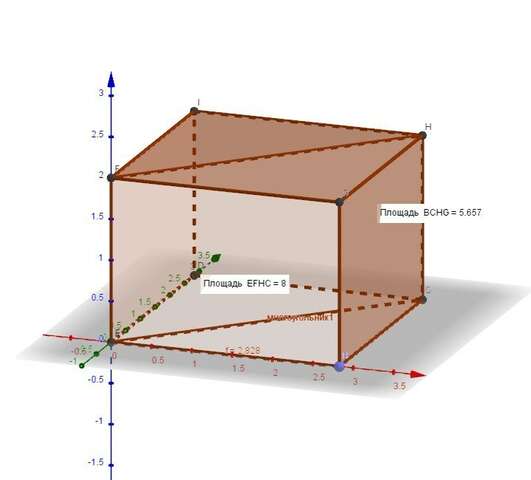
Площадь диагонального сечения правильной четырёхугольной призмы (Да, вообще, любой прямой четырёхугольной призмы) - прямоугольник.

=> Sди.сеч. = S1 = a*h = 8; где а - длина диагонали квадрата (основания)

h - высота призмы.

Так как призма правильная, то в основание квадрат = > по теореме Пифагора

a^2 = c^2 + c^2 где c - длина стороны квадрата.

=> c = $\frac{a}{\sqrt{2}}$

Площадь боковой поверхности можно найти P - периметр основания

Sб = P*h = 4c * h = $\frac{4*a*h}{\sqrt{2} }$ = 32/ $\sqrt{2}$ =

16 $\sqrt{2}$

Ответ: 16 $\sqrt{2}$