Около трапеции ABCD (BC||AD) описана окружность, и в ту же трапецию вписана другая...

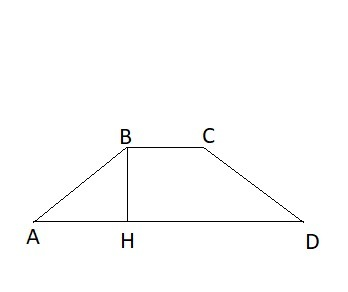
Если вокруг трапеции описана окружность, то она равнобедренная:

AB = CD

Если в четырехугольник вписана окружность, то суммы его противоположных сторон равны:

AD + BC = AB + CD = 2*AB

Из условия AD = 5*BC, подставим предыдущее равенство:

5*BC + BC = 2*AB

AB = 3*BC

$AH=\frac{AD-BC}{2}=\frac{5*BC-BC}{2}=2*BC$

Из прямоугольного ΔABH, по теореме Пифагора найдем высоту трапеции BH:

$BH=\sqrt{AB^2-AH^2}=\sqrt{(3*BC)^2-(2*BC)^2}=BC\sqrt{5}$

Подставим в формулу площади трапеции:

$S=\frac{AD+BC}{2}*BH=\frac{5*BC+BC}{2}*BC\sqrt{5}=3\sqrt{5}*BC^2\\BC^2=\frac{S}{3\sqrt{5}}=\frac{\frac{3\sqrt{5}}{5}}{3\sqrt{5}}=\frac{1}{5}\\BC=\frac{1}{\sqrt{5}}\\BH=BC*\sqrt{5}=1$