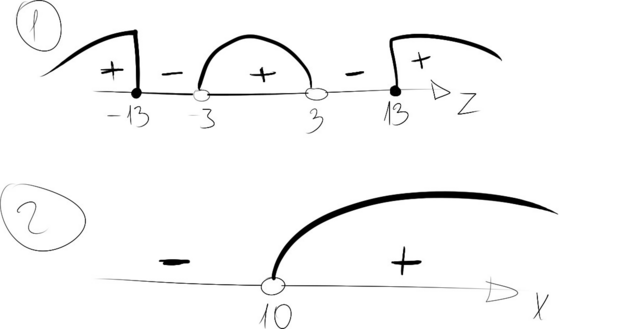
В первом задании по сути решение излишне. Рассмотрим числитель. Первая скобка ВСЕГДА больше нуля, поскольку по определению квадрат числа не может быть отрицательным или равным нулю. Вторая скобка напоминает разность квадратов, расписываем:
z² - 169 = z² - 13² = (z - 13) · (z + 13). Это будут вколотые (закрашенные) точки. Извините, если неправильно назвал таковую.
Переходим к знаменателю. Снова видим разность квадратов:
z² - 9 = z² - 3² = (z - 3) · (z + 3). Отмечаем эти точки как выколотые (не закрашенные). Из рисунка получаем, что:
z ∈ (-∞; -13] U (-3; 3) U [13; +∞)
Второе задание решается немного по-другому. Для начала требуется перенести единицу влево и привести к общему знаменателю:
0\\\\\\\frac{x + 13 - (x - 10)}{x - 10} > 0\\\\\\\frac{x + 13 - x + 10}{x - 10} >0\\\\\\\frac{23}{x - 10} > 0" alt="\tt\displaystyle \frac{x + 13}{x - 10} - 1 > 0\\\\\\\frac{x + 13 - (x - 10)}{x - 10} > 0\\\\\\\frac{x + 13 - x + 10}{x - 10} >0\\\\\\\frac{23}{x - 10} > 0" align="absmiddle" class="latex-formula">
Мы получили одну точку - это 10. Поскольку она находится в знаменателе, она выколотая. Из того же рисунка получаем, что:
x ∈ (10; +∞)
