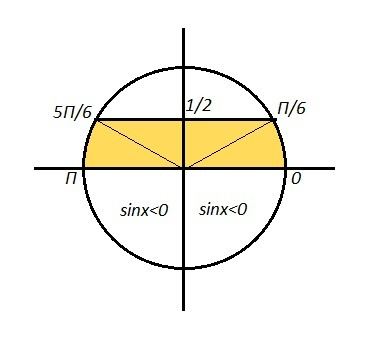
0\; ,\\\\\star \; \; log_4(sin^3x)=log_{2^2}(sinx)^3=\frac{3}{2}\cdot log_2(sinx)\; \; \star \\\\t=log_2(sinx)\; ,\; \; 4t^2+8t-1\geq 0\; ,\\\\D/4=16+9=25\; ,\; t_1=-1\; ,\; t_2=\frac{1}{9}\\\\4(t+1)(t-\frac{1}{9})\geq 0\; \; ,\quad +++(-1)---(\frac{1}{9})+++\\\\t\leq -1\; \; \; ili\; \; \; t\geq \frac{1}{9}\\\\a)\; \; log_2(sinx)\leq -1\; \; ,\; \; sinx\leq 2^{-1}\; ,\; \; sinx\leq \frac{1}{2}\; ,\; \; 00\; ,\\\\\star \; \; log_4(sin^3x)=log_{2^2}(sinx)^3=\frac{3}{2}\cdot log_2(sinx)\; \; \star \\\\t=log_2(sinx)\; ,\; \; 4t^2+8t-1\geq 0\; ,\\\\D/4=16+9=25\; ,\; t_1=-1\; ,\; t_2=\frac{1}{9}\\\\4(t+1)(t-\frac{1}{9})\geq 0\; \; ,\quad +++(-1)---(\frac{1}{9})+++\\\\t\leq -1\; \; \; ili\; \; \; t\geq \frac{1}{9}\\\\a)\; \; log_2(sinx)\leq -1\; \; ,\; \; sinx\leq 2^{-1}\; ,\; \; sinx\leq \frac{1}{2}\; ,\; \; 0
1\; \; \Rightarrow \; \; x\in \varnothing \\\\Otvet:\; \; x\in (2\pi n\, ;\, \frac{\pi }{6}+2\pi n\, ]\cup [\, \frac{5\pi }{6}\, ;\, \pi +2\pi n)\; ,\; n\in Z" alt="x\in (2\pi n\, ;\, \frac{\pi }{6}+2\pi n\, ]\cup [\, \frac{5\pi }{6}\, ;\, \pi +2\pi n)\; \; ,\; n\in Z\\\\b)\; \; log_2(sinx)\geq \frac{1}{9}\; \; ,\; \; sinx\geq 2^{1/9}\; \; \; i\; \; \; 01\; \; \Rightarrow \; \; x\in \varnothing \\\\Otvet:\; \; x\in (2\pi n\, ;\, \frac{\pi }{6}+2\pi n\, ]\cup [\, \frac{5\pi }{6}\, ;\, \pi +2\pi n)\; ,\; n\in Z" align="absmiddle" class="latex-formula">
