В треугольнике ABC угол С равен 90 градусов,CH - высота,AB = 17,tg A=1/4.Найдите BH.

Question 1

Question 2

Ответ:

BH = 1 (единиц)

Пошаговое объяснение:

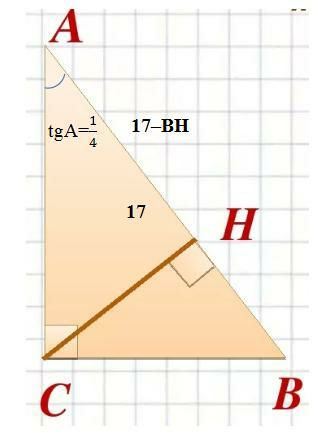
Дано (см. рисунок):

ΔABC

∠C=90°

CH - высота

AB = 17

tg A = 1/4

Найти: BH

Решение.

Так как CH - высота, то её можно выразить через проекции катетов на гипотенузу: $\displaystyle CH^{2}=AH*BH$

Так как AH=17–BH, то $\displaystyle CH^{2}=(17-BH)*BH$ .

С другой стороны:

tg A=CH/AH или CH= AH•tg A = AH/4=(17–BH)/4.

Тогда

$\displaystyle (\frac{(17-BH)}{4} )^{2}=(17-BH)*BH$ или

$\displaystyle \frac{(17-BH)^{2}}{16} =(17-BH)*BH$

Но BH<17, то есть 17–BH>0 и поэтому

$\displaystyle \frac{(17-BH)}{16}=BH$ или

17–BH=16·BH

17·BH=17

BH=1.

axatar_zn · Answer 1 · 2020-05-26T08:52:28+0000