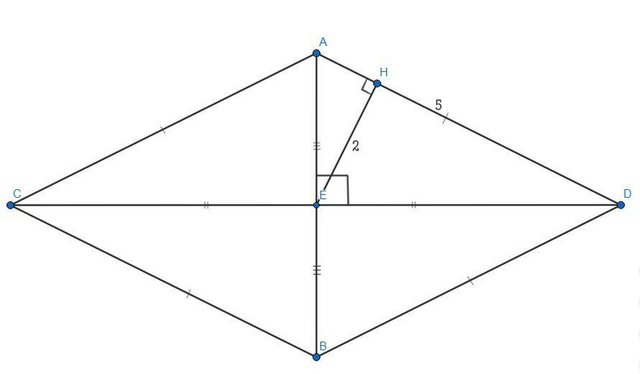
-Рисунок смотрите в приложении-
Дано:
ABCD - ромб.
АВ и CD - диагонали.
Точка Е - точка пересечения АВ и CD.
ЕН - расстояния от центра ромба до стороны = 2.
AD = 5.
Найти:
S(ABCD) = ?
Решение:
- Точка пересечения диагоналей ромба - центр ромба. В данном случае центр ромба - точка Е.
- Диагонали ромба точкой пересечения делятся пополам (по свойству параллелограмма), но также они взаимно перпендикулярны (по свойству ромба). Из этих свойств следует, что диагонали ромба, пересекаясь, образуют четыре равных прямоугольных треугольника. В нашем случае - ΔСАЕ = ΔADE = ΔDBE = ΔCВЕ.
- Рассмотрим ΔЕАD прямоугольный. ЕН - высота. Площадь треугольника равна половине произведения его стороны и высоты, проведённой к этой стороне. Следовательно, S(ΔEAD) = 0,5*EH*AD = 0,5*2*5 = 5 (ед²).
- Выше было сказано, что все четыре прямоугольных треугольника, образованных пересечением диагоналей, равны. У равных многоугольников равны их площади (по свойству площадей многоугольников). Ромб состоит из этих 4 равных треугольников, поэтому, чтобы найти его площадь, нужно просто умножить площадь ΔEAD на 4.
- Итак, S(ABCD) = S(ΔEAD)*4 = 5 (ед²)*4 = 20 (ед²).
Ответ: 20 (ед²).