Ответ: 50 см²
Пошаговое объяснение:
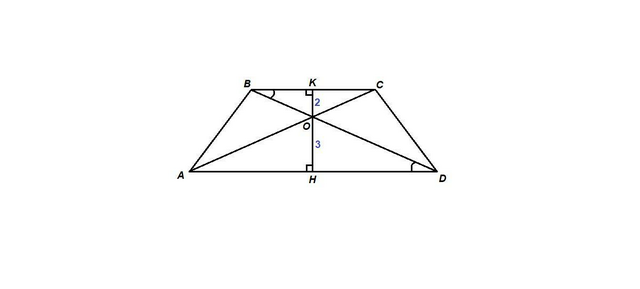
О - точка пересечения диагоналей.
Расстояние от точки О до оснований - длины перпендикуляров, проведенных из О к основаниям:
ОК = 2 см, ОН = 3 см.
Тогда КН = 5 см - высота трапеции.
∠СВО = ∠АDО как накрест лежащие при пересечении параллельных прямых AD и ВС секущей AD,
∠СОВ = ∠AOD как вертикальные, значит
ΔСОВ ~ ΔAOD по двум углам.
В подобных треугольниках отношение высот, проведенных к соответствующим сторонам, равно коэффициенту подобия, значит


 см
см
 см²
см²