Диагональ осевого сечения цилиндра равна 121 см, радиус основания 6√2 см. Найдите высоту...

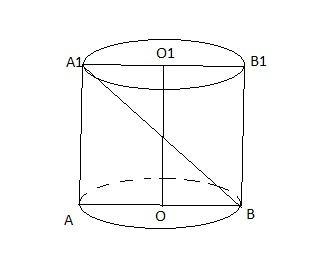
Проведем сечение ABB1A1 цилиндра через его ось OO1.

По условиям задачи диагональ осевого сечения BA1 равна 121 см, а радиус основания OA = 6√2 см

Зная радиус найдем диаметр основания AB = 2 * OA = 2 * 6√2 = 12√2 см

Из прямоугольного ΔAA1B найдем высоту цилиндра AA1:

$AA_1=\sqrt{BA^2_1-AB^2}=\sqrt{121^2-(12\sqrt{2})^2}=\sqrt{14353}\approx119.8$

Ответ: Высота цилиндра примерно 119.8 см