В выпуклом четырехугольнике KLMN лучи LK и MN пересекаются под углом 25∘. Лучи LM и KN,...

Question

В выпуклом четырехугольнике KLMN лучи LK и MN пересекаются под углом 25∘. Лучи LM и KN, пересекаются под тем же углом 25∘. Найдите следующую разность ∠MNK−∠MLK. Ответ дайте в градусах.

Answer 1

Ответ:    50°

Пошаговое объяснение:

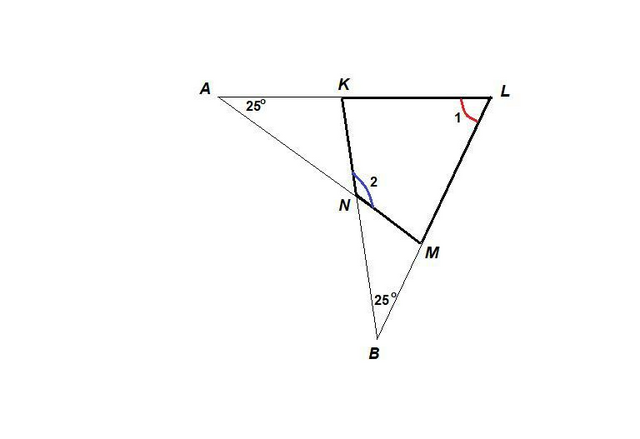
Пусть LK ∩ MN = A,   LM ∩ KN = B.

Из ΔАМL:

∠AML = 180° - ∠A - ∠1 = 180° - 25° - ∠1 = 155° - ∠1

Из ΔBKL:

∠BKL = 180° - ∠B - ∠1 = 180° - 25° - ∠1 = 155° - ∠1

Сумма углов выпуклого четырехугольника равна 360°.

∠2 = 360° - (∠NML + ∠NKL + ∠1)

∠2 = 360° - (155° - ∠1) - (155° - ∠1) - ∠1

∠2 = 360° - 310° + ∠1

∠2 = 50° + ∠1

∠2 - ∠1 = 50°

∠MNK - ∠MLK = 50°

---