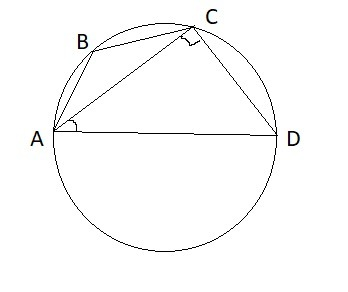
Т.к. ∠ACD опирается на диаметр окружности, то ∠ACD = 90°
Т.к. четырехугольник ABCD вписан в окружность, то сумма его противоположных углов равна 180°
∠ABC + ∠ADC = 180° ⇒ ∠ADC = 180° - ∠ABC =180° - 134° = 46°
Сумма углов ΔACD равна 180°
∠CAD + ∠ACD + ∠ADC = 180° ⇒ ∠CAD = 180° - ∠ACD - ∠ADC = 180° - 90° - 46° = 44°