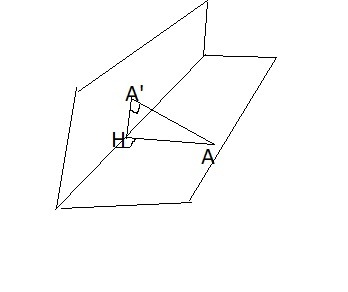
Расстояние от точки A до второй плоскости - это величина перпендикуляра AA' опущенного из точки A на вторую плоскость. Расстояние от точки A до линии пересечения плоскостей это величина перпендикуляра AH опущенного из точки A на прямую пересечения.
Соединив точки A' и H получим прямоугольный треугольник AA'H (т.к. AA' перпендикулярен любой прямой второй плоскости. По теореме о 3 перпендикулярах A'H будет перпендикулярен и прямой пересечения, а следовательно является проекцией AH на вторую плоскость и в таком случае угол AHA' и будет углом между двумя плоскостями.
Из прямоугольного ΔAHA' найдем