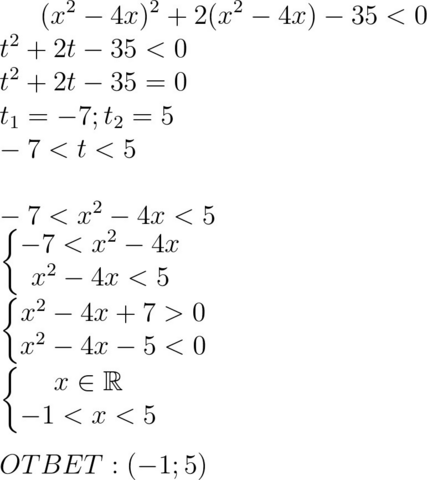1. Сделаем замену (x² - 4x) = t
2. Решим неравенство относительно t (методом интервалов)
3. Осуществим обратную замену
4. Найдём значения x
1) В первом квадратном неравенстве с x D<0, a>0 ⇒ данное неравенство верно при любом x
2) Решается методом интервалов, аналогично неравенству с t