В выпуклом четырёхугольнике ABCD точки E, F и G — середины сторон AB, BC и AD...

Question

В выпуклом четырёхугольнике ABCD точки E, F и G — середины сторон AB, BC и AD соответственно, причём GE⊥AB, GF⊥BC. Найдите угол ACD. В качестве ответа введите число, чему равен угол ACD в градусах.

Answer 1

Ну, давай разбираться!

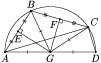
1-ое мое действие нарисовал рисунок( то, что происходит в задаче)

2-ое действие будем рассматривать два треугольника, а именно AGB и BGC: и видим, что GE-медиана, высота и биссектриса треугольника AGB, GF-аналогично =>

DG = AG = BG = CG => G – центр окружности, описанной около данного четырёхугольника ABCD.  ∠ACD = 90°,  так как он э вписанный угол, опирающийся на диаметр окружности

Ответ : ∠ACD = 90°

---

Comments

Баальшое спасибо!!!