Часть графика линейной функции, расположенная во второй координатной четверти, вместе с...

Question

Часть графика линейной функции, расположенная во второй координатной четверти, вместе с осями координат образует треугольник. Во сколько раз изменится его площадь, если угловой коэффициент функции в 2 раза увеличить, а свободный член в два раза уменьшить?

Answer 1

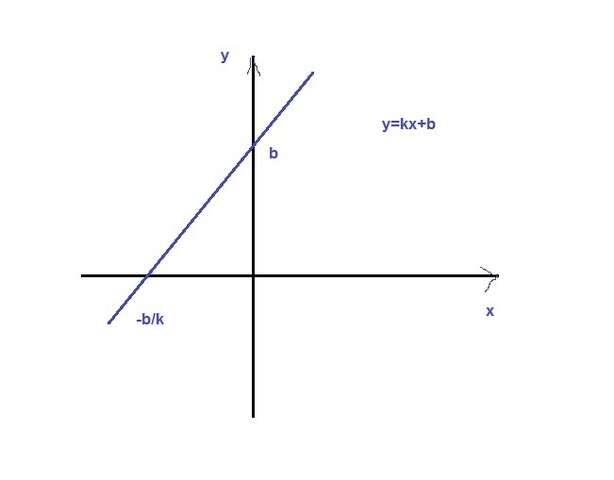
Ответ:

треугольник прямоугольный с катетом =b

найдем другой катет    при у=0 ; kx+b=0  x=-b/k длину катета берем по модулю = b/k

площадь исходного треугольника S=(1/2)b*b/k =(1/2)b²/k

площадь измененного треугольника S1=(1/2) ( b/2)²/(2k)=((1/2)b²/k)/8=S/8

площадь уменьшится в 8 раз

---