Пошаговое объяснение:
1. Необходимое условие экстремума - первая производная функции равна 0. Скорость изменения функции равна 0.
2.
3. Уравнение прямой: y = k*x + b.
k = tgα = tg45° = 1 - коэффициент наклона прямой.
b = y - k*x. Проводим через точку М(2;1), где Му=1, Мх=2
b = My - k*Mx = 1 - 1*2 = - 1.
Получили уравнение: у = x - 1 - ответ.
4. Разложили знаменатель на (х-5)*(х+5) и сократили дробь на (х+5).
Получили y= 1/(x-5), подставили х = -5 и результат:
lim(-5) У = 1/(-5-5) = - 1/10 = -0,1 - ответ
5.
ВАЖНО: возрастает там, где первая производная функции положительна.
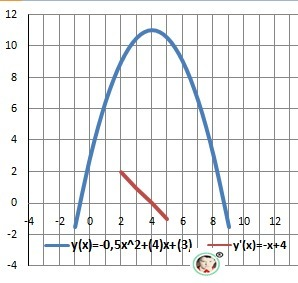
Y(x) = -1/2*x² + 4*x +3 - функция
Y'(x) =Ва - (1/2)*2* x+ 4*1 = - x + 4 = 0 - производная - график прямая линия.
Х = 4 - экстремум - максимум.
Важно: Функция парабола с отрицательным коэффициентом - ветви у неё вниз - возрастает до экстремума.
Возрастает: Х∈(-∞;4), максимум: У(4), убывает: Х∈(4;+∞) - ответ.
Рисунок к задаче в приложении - подарок.
Или второй вариант решения: привести уравнение формулы к виду:
y = -(x-4)² + 12 и координата вершины параболы: А(4;12) и максимум при Х=4.
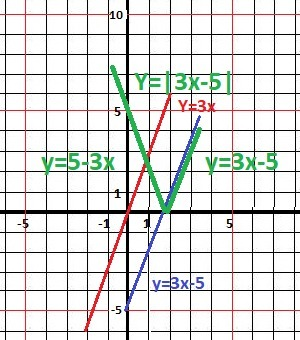
5. Важно: при построении графиков с модулем - отрицательную часть графика зеркально отражаем относительно оси ОХ.
Рисунок с графиком в приложении.
Последовательное преобразование графиков приводит к двум участкам: y = 5-3x y = 3x+5