Пошаговое объяснение:
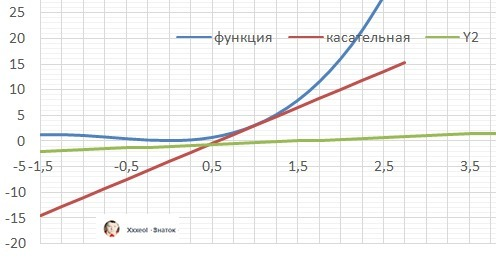
1. Находим уравнение касательной (достаточно только коэффициент наклона)
k = Y'(x) = 3*x² + 4*x
Вычисляем при х = Xo=1
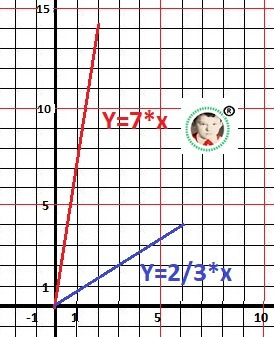
k(Xo) = k(1) = 3 + 4 = k1 = 7 - наклон первой прямой (касательной). Y= 7*x - 4/
2. Находим коэффициент наклона второй прямой.
3*y = 2*x - 3
y = 2/3*x - 1. k2 = 2/3 -
3. Угол между касательными находим по формуле "разность тангенсов".
tg(α) = (7-2/3)/(1+ 4*2/3) = 1 2/17 = 1.118
Угол - arctg(1.118) = 0.841 = 48.18° - ответ
Рисунки к задаче в приложении. Удивительно, но очень походе на угол в 48 градусов.