Ответ "силой Разума" - "ответ Замятина"
Дано: Y(x) = (x³ + 6*x²)⁽¹/³⁾ - функция.
Пояснения:
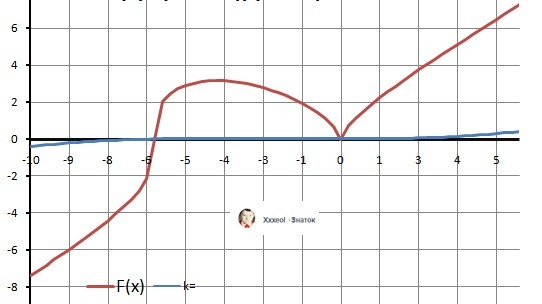
1. На рисунке 1 - самое интересное в этой функции - её центральная и проблемная часть. Можно просто любоваться, а я первый раз график такой функции построил, как она изгибается в области от 0 до -6.
2. Вертикальной асимптоты нет - нет разрыва - это правильно.
3. У горизонтальной асимптоты нет наклона, и, поэтому нет - k=1.
Уравнение горизонтальной асимптоты: Y = x - константа.
Вычисляется по формуле: lim(-∞) Y(x) = lim(+∞) Y(x) - именно два предела с разных сторон. В этой части вопроса автор немного ошибается.
Горизонтальных асимптот - нет.
4. Переходим к поиску наклонной асимптоты по уравнению:
y = k*x+ b.
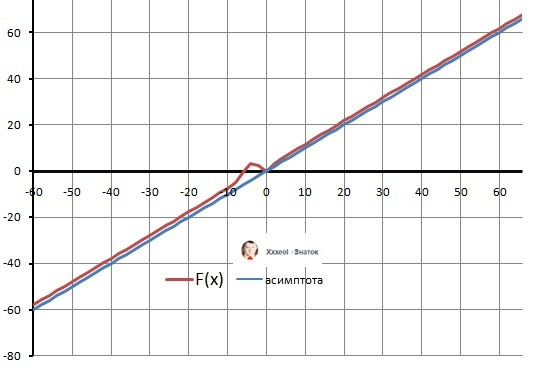
Наклон - lim(∞)Y(x)/x = 1 - это правильно и ... смотрим рисунок 2 в приложении.
И здесь начинается борьба физики, но не с лирикой, а с математикой.
"Физикам" достаточно уравнения: Y(x) = k*x, потому, что это предел функции, На бесконечных расстояниях какое-то конкретное число b - не имеет никакого физического смысла. Примерно, как миллиард миллиардов километров плюс 2 километра.
4. Вычисляем сдвиг b - асимптоты.
b = lim(→∞)(Y(x) - x) =
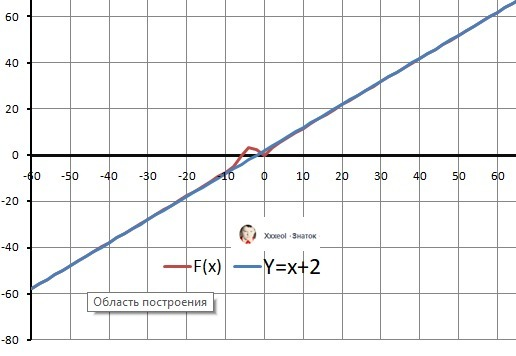
Расчет показывает: b = 0, но b = 2 -лучше.
И это видно на рисунке 2 приложения.