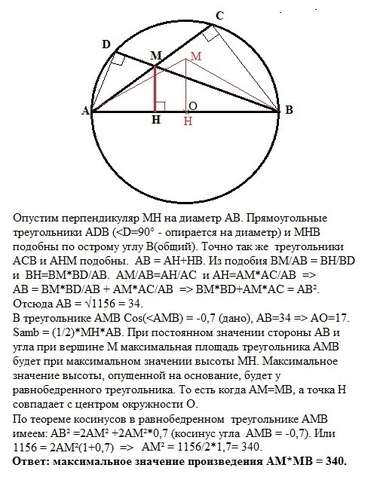
Опустим перпендикуляр МН на диаметр АВ. Прямоугольные треугольники ADB (
АВ = ВМ*BD/AB + АМ*АС/АВ => BM*BD+AM*AC = AB².
Отсюда АВ = √1156 = 34.
В треугольнике АМВ Cos( АО=17.
Samb = (1/2)*MH*AB. При постоянном значении стороны АВ и угла при вершине М максимальная площадь треугольника АМВ будет при максимальном значении высоты МН. Максимальное значение высоты, опущенной на основание, будет у равнобедренного треугольника. То есть когда АМ=МВ, а точка Н совпадает с центром окружности О.
По теореме косинусов в равнобедренном треугольнике АМВ имеем: АВ² =2АМ² +2АМ²*0,7 (косинус угла АМВ = -0,7). Или 1156 = 2АМ²(1+0,7) => АМ² = 1156/2*1,7= 340.
Ответ: максимальное значение произведения АМ*МВ = 340.