Можете, пожалуйста, объяснить решение данной задачи. Желательно с чертежом. И если будут...

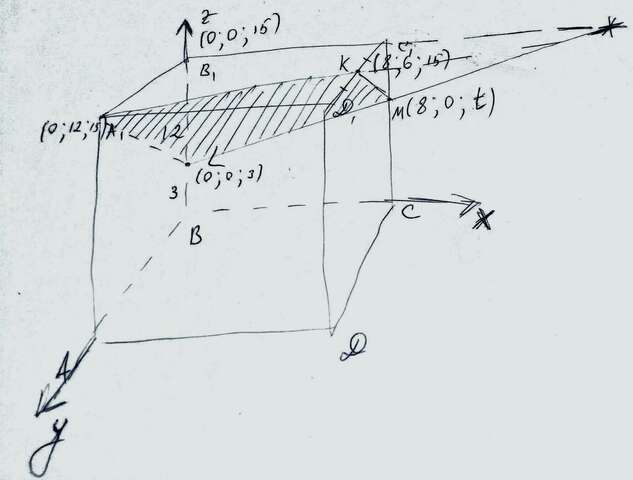
Решаем координатным методом. (мой кривенький чертеж в прикрепе)

а) Для начала нужно найти уравнение плоскости LKA₁. Плоскости принадлежат точки L (0; 0; 3), K(8; 6; 15), A₁ (0; 12; 15). Составляем систему уравнений.

$\left \{ \begin{array}{I} 3c+d=0 \\ 12b+15c+d=0 \\ 8a+6b+15c+d=0 \end{array} \ \Rightarrow \ \left \{ \begin{array}{I} c=-\dfrac{d}{3} \\ b=\dfrac{d}{3} \\ a=\dfrac{d}{4} \end{array}$

Получим уравнение плоскости

$\dfrac{1}{4}x+\dfrac{1}{3}y-\dfrac{1}{3}z+1=0$

Обозначим место пересечения CC₁ и плоскости как M. Ее координаты (8; 0; t). t найдем, подставив все в уравнение плоскости.

$2+0-\dfrac{t}{3}+1=0 \\ \dfrac{t}{3}=3 \\ t=9$

Значит точка M делит CC₁ в отношении (15-9)/9=6/9=2/3

б) Косинус угла между плоскостями, это косинус между их верторами нормали, взятый по модулю. Плоскость A₁B₁C₁ параллельна плоскости xOy, значит a и b равны нулю, c найдем из точки B₁.

$15c+d=0 \ \Rightarrow \ c=-\dfrac{d}{15}$

Получим уравнение плоскости A₁B₁C₁

$-\dfrac{z}{15}+1=0$

Тогда векторы имееют координаты

плоск. LKA₁: n {1/4; 1/3; -1/3}

плоск. A₁B₁C₁: n {0; 0; -1/15}

И можно посчитать косинус

$cos \varphi =\left|\dfrac{0+0+-\frac{1}{15}\cdot \left(-\frac{1}{3}\right)}{\sqrt{(\frac{1}{4})^2+(\frac{1}{3})^2+(-\frac{1}{3})^2\cdot \sqrt{0+0+(-\frac{1}{15})^2}}}\right|=\dfrac{12\cdot15}{45\cdot\sqrt{41}}=\bf\dfrac{4}{\sqrt{41}}$

Ответ: а) 2/3, б) 4/√41