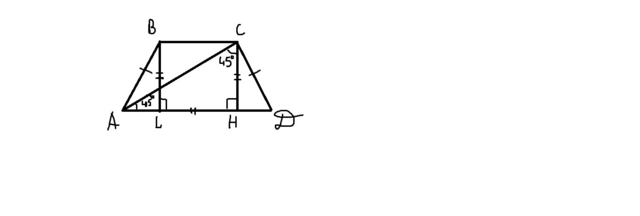
1). Рассмотрим равнобедренную трапецию ABCD. Из точки С опустим высоту СH на сторону AD;
2). Рассмотрим прямоугольный треугольник ACH. ∠CAH=45° по условию, тогда ∠ACH=180°-∠CAH-∠CHA=180°-45°-90°=45° (сумма углов треугольника равна 180°). Получаем, что ∠CAH=∠ACH=45°⇒прямоугольный треугольник ACH равнобедренный⇒AH=HC.
3). Рассмотрим прямоугольный равнобедренный треугольник ACH. По теореме Пифагора:
AH²+HC²=AC²;
Т.к. из пункта 2 следует, что AH=HC, то:
2*AH²=AC²;
Т.к. AC=8√2 по условию, то:
2*AH²=128;
AH²=64;
AH=HC=8;
4). Рассмотрим равнобедренную трапецию ABCD. Из точки B опустим высоту BL на сторону AD;
5). Рассмотрим прямоугольный треугольник ALB. По теореме Пифагора:
AL²+BL²=AB²
В равнобедренной трапеции ABCD высоты BL и CH равны и параллельны, как расстояния между параллельными прямыми BC и AD. BL=CH=8 (из пункта 3). Тогда:
AL²+64=AB²;
6). В равнобедренной трапеции ABCD фигура BLHC - прямоугольник, т.к. BL=CH и BL || CH⇒BC=LH, как противоположные стороны прямоугольника;
7). AL=AH-LH=AH-BC. Т.к. AH=8 (пункт 3), то AL=8-BC;
8). Подставив вычисления из пункта 7 в пункт 5, получаем:
(8-BC)²+64=AB²
9). Т.к. по условию AB-BC=8, то AB=8+BC, тогда:
(8-BC)²+64=(8+BC)²;
64-16*BC+BC²+64=64+16*BC+BC²;
-16*BC+64=16*BC
32*BC=64
BC=2
Т.к. BC=LH (пункт 6), то LH=2
10). Рассмотрим равнобедренную трапецию ABCD. Прямоугольный треугольник ABL равен прямоугольному треугольнику DCH по катету и прилежащему к нему острому углу, а именно:
а). AB=CD, т.к. трапеция ABCD равнобедренная;
б). ∠BAL=∠CDH, т.к. трапеция ABCD равнобедренная.
Из равенства треугольников следует равенство соответственных элементов, т.е. AL=HD, как соответственные катеты.
11). Рассмотрим сторону AD в равнобедренной трапеции ABCD.
AD=AL+LH+HD;
AL=HD=AH-LH;
Из пункта 3 AH=8, из пункта 9 LH=2, тогда:
AL=HD=8-2=6;
AD=6+2+6=14, что и требовалось найти.
Ответ: AD=14.