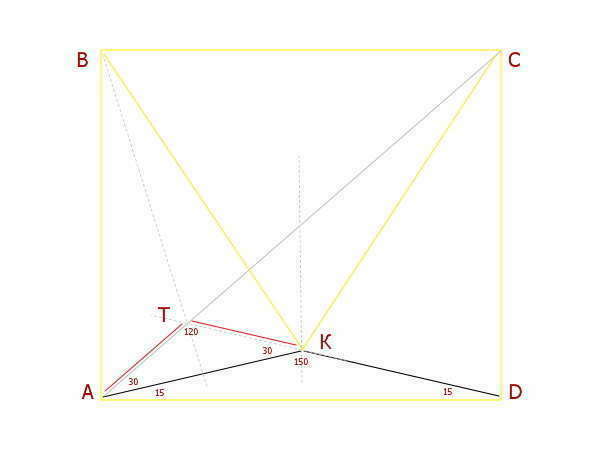
Т.к. углы равны КAD = KDA => AKD -- равнобедренный
треугольники AKВ и DKC равны по двум сторонам и углу между ними
(BA=CD --- т.к. квадрат, АК=KD --- т.к. AKD равнобедренный,
угол ВАК=CDK = 90-15 = 75 градусов)))
=> BK = KC
понятно, что нужно поискать треугольник с углами 30 и 60 градусов
(желательно прямоугольный...)))
если продолжить сторону KD до пересечения с диагональю АС
(точку пересечения обозначим Т) --- получится треугольник АТD
с углами 15, 45, 120... (диагонали квадрата взаимно перпендикулярны и являются биссектрисами его углов)))
соединим точки В и Т прямой линией...
и рассмотрим получившиеся треугольники
угол ТАК=30=ТКА
=> BT _|_ AK
и в треугольнике АТК эта прямая --- медиана,
значит и для АВК эта прямая ВТ и медиана и высота,
т.е. АВК --- равнобедренный и АВ=ВК=а
(((здесь самое тонкое место следующий вывод:
из доказанной равнобедренности меньшего треугольника АТК
сделать вывод о равнобедренности бОльшего треугольника АВК...
обычно рассуждения следуют в обратном порядке...
но здесь прямая ВТ по построению содержит медиану треугольника АТК --- вторую точку не обозначила, пусть ТХ будет...
это одна прямая линия...)))