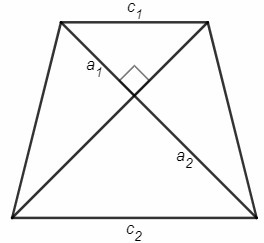
Площадь четырехугольника с перпендикулярными диагоналями равна полупроизведению диагоналей. Так как диагонали равнобедренной трапеции равны S=d^2/2 => d=√(144*2)=12√2
Диагонали трапеции образуют на основаниях подобные треугольники.
a1+a2=12√2
a1/a2 =с1/с2 =3/5
Диагонали равны, разделены в равном отношении, следовательно образованные треугольники равнобедренные. Стороны в равнобедренных прямоугольных треугольниках относятся как 1:1:√2
c1=3/8 *12√2 *√2 =3*3=9
c2=5/8 *12√2 *√2 =5*3=15