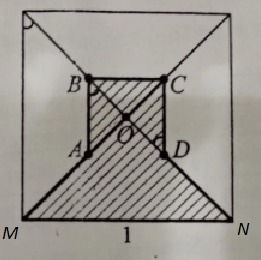
A.14. Заштрихованная область состоит из ΔMON и четырёх равных треугольников АОВ , ВОС , СОD ( см. рис.) .
ΔMON: MN=1 - это сторона квадрата, диагонали которого - удвоенные отрезки МО и NO . Диагональ квадрата со стороной а=1 по теореме Пифагора равна d=√(1²+1²)=√2 . Тогда МО=NO=√2/2. Диагонали квадрата пересекаются под углом в 90°, поэтому ΔMON - прямоугольный, его площадь равна полупроизведению катетов: S=1/2*(√2/2)*(√2/2)=2/8=1/4 .
ΔАОВ, ΔВОС и ΔCOD - равные прямоугольные треугольники с катетами, равными ОА=ОВ=ОС=ОD=х . Площадь каждого такого треугольника равна S=1/2*x*x=(1/2)*x^2 . А площадь всех трёх треугольников равна (3/2)*х² .
Заштрихованная фигура имеет площадь, равную 1/4+(3/2)*х² . Ответ под №2 .
А.15. Номера уравнений, которые не имеют решений - 2 и 4, так как функции y=sinx и y=cosx принимают значения в промежутке [-1 ; 1] , а числа (6/5)>1 и 2arctg1=2*(П/4)=П/2≈(3,14/2)=1,57>1 .