Определение 1. Двугранным углом называется фигура, образованная двумя не принадлежащими одной плоскости полуплоскостями, имеющими общую границу – прямую а
Определение 2. Линейным углом двугранного угла называется плоский угол, образованный двумя лучами, которые лежат в гранях этого двугранного угла и перпендикулярны его ребру.
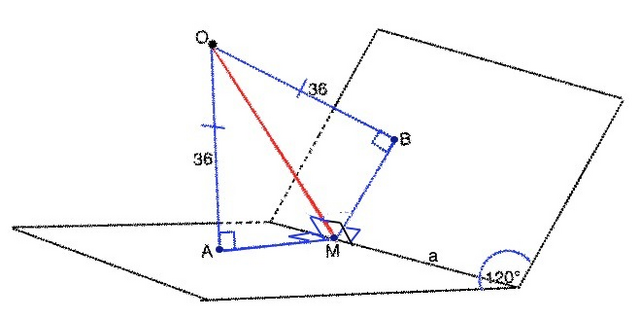
Решение. Обозначим перпендикуляр на одну грань ОА, на другую = ОВ. Расстояние от точки до прямой - отрезок, проведенный перпендикулярно к прямой. Проведем перпендикуляр ОМ, к ребру двугранного угла. ОМ - наклонная к граням этого угла. По т. о 3-х перпендикулярах АМ и ВМ – проекции ОМ и перпендикулярны ребру а, угол АМВ=120°. ОМ – является гипотенузой прямоугольных ∆ ОАМ и ∆ ОВМ. Эти треугольники равны по катету (ОА=ОВ по условию) и общей гипотенузе. => Угол ОМВ=ОМА=120:2=60°. Тогда ОМ=ОА:sin60°=36:(√3/2)= 24√3 дм.