Основания равнобедренной трапеции равны 9 и 15.Тангенс острого угла равен 3.Найдите...

Ответ:

Пошаговое объяснение:

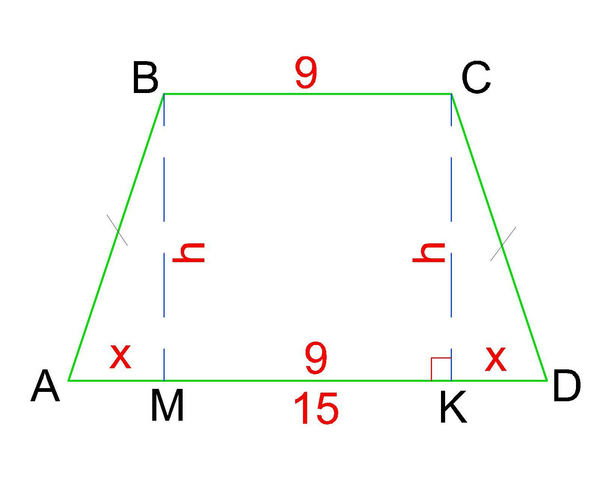
Построим равнобокую трапецию ABCD, основаниями BC=9, DA=15 и боковыми сторонами AB=CD.

Опустим 2 высоты BM и CK на основание AD. Получили 2 равных прямоугольных ΔABM=ΔDCK. Равенство треугольников следует из того, что ∠А=∠D, ∠AMB=∠DKC=90° ⇒ ∠ABM=∠DCK и сторона AB=CD (треугольники равны по второму признаку равенства).

Т.к. ΔABM=ΔDCK, то MA=KD=x.

MK=BC=9 (т.к. BC║AD и BM⊥AD и CK⊥AD)

Тогда $x=\frac{AD-BC}{2} =\frac{15-9}{2} =3$

Рассмотрим прямоугольный ΔDCK. В нём острый ∠CDK - это острый угол трапеции, катет CK=h, лежит напротив острого ∠CDK, катет KD=3 - прилежащий к острому ∠CDK.

Так как тангенс угла есть отношение противолежащего этому углу катета к прилежащему, то

$tg\angle CDK=\frac{CK}{KD} =\frac{h}{3} =3$

⇒ h=3*3=9