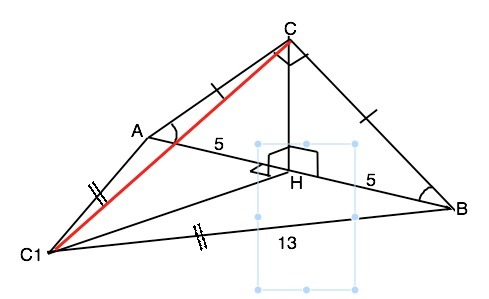
Плоскости ∆ АВС и АВС1 перпендикулярны, т.е. образуют двугранный угол 90°. Значит, плоский угол СНС1, образованный высотами этих треугольников, которые лежат в гранях этого двугранного угла и перпендикулярны его ребру, равен 90°. Искомый отрезок СС1 - гипотенуза прямоугольного треугольника СНС1. Чтобы вычислить ее длину, найдем катеты этого треугольника. В ∆ АВС с гипотенузой АВ=10 высота СН является и медианой, поэтому равна АН=ВН=10:2=5 см (свойство медианы прямоугольного треугольника). Из ∆ АС1В по т.Пифагора С1Н=√(АC1²-АН²)=√(13²-5²)=12 см. Треугольники АНС1 и СНС1 равны по равенству катетов. ⇒ СС1=АС1=13 см