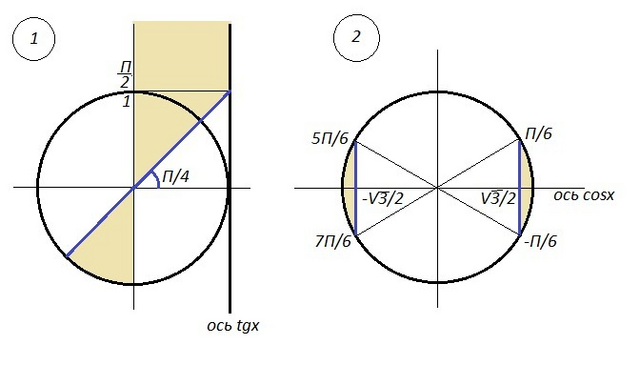
![1)\; \; tg(\frac{\pi}{6}-2x)\geq 1\\\\\frac{\pi }{4}+\pi n\leq \frac{\pi }{6}-2x<\frac{\pi}{2}+\pi n\; ,\; n\in Z\\\\\frac{\pi}{4}-\frac{\pi}{6}+\pi n\leq -2x<\frac{\pi }{2}-\frac{\pi}{6}+\pi n\\\\\frac{\pi}{12}+\pi n\leq -2x<\frac{2\pi}{6}+\pi n\\\\-\frac{\pi}{3}+\pi n<2x\leq -\frac{\pi }{12}+\pi n\\\\-\frac{\pi}{6}+\frac{\pi n}{2}<x\leq -\frac{\pi}{24}+\frac{\pi n}{2}\\\\Otvet:\; \; x\in (-\frac{\pi}{6}+\frac{\pi n}{2}\; ;\; -\frac{\pi}{24}+\frac{\pi n}{2}\, ] \;\; ,\; n\in Z .](https://tex.z-dn.net/?f=1%29%5C%3B%20%5C%3B%20tg%28%5Cfrac%7B%5Cpi%7D%7B6%7D-2x%29%5Cgeq%201%5C%5C%5C%5C%5Cfrac%7B%5Cpi%20%7D%7B4%7D%2B%5Cpi%20n%5Cleq%20%5Cfrac%7B%5Cpi%20%7D%7B6%7D-2x%3C%5Cfrac%7B%5Cpi%7D%7B2%7D%2B%5Cpi%20n%5C%3B%20%2C%5C%3B%20n%5Cin%20Z%5C%5C%5C%5C%5Cfrac%7B%5Cpi%7D%7B4%7D-%5Cfrac%7B%5Cpi%7D%7B6%7D%2B%5Cpi%20n%5Cleq%20-2x%3C%5Cfrac%7B%5Cpi%20%7D%7B2%7D-%5Cfrac%7B%5Cpi%7D%7B6%7D%2B%5Cpi%20n%5C%5C%5C%5C%5Cfrac%7B%5Cpi%7D%7B12%7D%2B%5Cpi%20n%5Cleq%20-2x%3C%5Cfrac%7B2%5Cpi%7D%7B6%7D%2B%5Cpi%20n%5C%5C%5C%5C-%5Cfrac%7B%5Cpi%7D%7B3%7D%2B%5Cpi%20n%3C2x%5Cleq%20-%5Cfrac%7B%5Cpi%20%7D%7B12%7D%2B%5Cpi%20n%5C%5C%5C%5C-%5Cfrac%7B%5Cpi%7D%7B6%7D%2B%5Cfrac%7B%5Cpi%20n%7D%7B2%7D%3Cx%5Cleq%20-%5Cfrac%7B%5Cpi%7D%7B24%7D%2B%5Cfrac%7B%5Cpi%20n%7D%7B2%7D%5C%5C%5C%5COtvet%3A%5C%3B%20%5C%3B%20x%5Cin%20%28-%5Cfrac%7B%5Cpi%7D%7B6%7D%2B%5Cfrac%7B%5Cpi%20n%7D%7B2%7D%5C%3B%20%3B%5C%3B%20-%5Cfrac%7B%5Cpi%7D%7B24%7D%2B%5Cfrac%7B%5Cpi%20n%7D%7B2%7D%5C%2C%20%5D%20%5C%3B%5C%3B%20%2C%5C%3B%20n%5Cin%20Z%20. "1)\; \; tg(\frac{\pi}{6}-2x)\geq 1\\\\\frac{\pi }{4}+\pi n\leq \frac{\pi }{6}-2x<\frac{\pi}{2}+\pi n\; ,\; n\in Z\\\\\frac{\pi}{4}-\frac{\pi}{6}+\pi n\leq -2x<\frac{\pi }{2}-\frac{\pi}{6}+\pi n\\\\\frac{\pi}{12}+\pi n\leq -2x<\frac{2\pi}{6}+\pi n\\\\-\frac{\pi}{3}+\pi n<2x\leq -\frac{\pi }{12}+\pi n\\\\-\frac{\pi}{6}+\frac{\pi n}{2}<x\leq -\frac{\pi}{24}+\frac{\pi n}{2}\\\\Otvet:\; \; x\in (-\frac{\pi}{6}+\frac{\pi n}{2}\; ;\; -\frac{\pi}{24}+\frac{\pi n}{2}\, ] \;\; ,\; n\in Z .")
3\\\\4cos^2\frac{x}{2}-3>0\\\\(2\, cos\frac{x}{2}-\sqrt3)\cdot (2\, cos\frac{x}{2}+\sqrt3)>0\\\\t=cos\frac{x}{2}\; ,\; \; (2t-\sqrt3)\cdot (2t+\sqrt3)>0\; \; ,\; \; +++(-\frac{\sqrt3}{2})---(\frac{\sqrt3}{2})+++\\\\t<-\frac{\sqrt3}{2}\; \; \; ili\; \; \; t>\frac{\sqrt3}{2}\\\\a)\; \; cos\frac{x}{2}<-\frac{\sqrt3}{2}\\\\\frac{5\pi }{6}+2\pi n<\frac{x}{2}<\frac{7\pi }{6}+2\pi n\; ,\; n\in Z\\\\\frac{5\pi }{3}+4\pi n<x<\frac{7\pi }{3}+4\pi n\\\\b)\; \; cos\frac{x}{2}>\frac{\sqrt3}{2}" alt="2)\; \; 4cos^2\frac{x}{2}>3\\\\4cos^2\frac{x}{2}-3>0\\\\(2\, cos\frac{x}{2}-\sqrt3)\cdot (2\, cos\frac{x}{2}+\sqrt3)>0\\\\t=cos\frac{x}{2}\; ,\; \; (2t-\sqrt3)\cdot (2t+\sqrt3)>0\; \; ,\; \; +++(-\frac{\sqrt3}{2})---(\frac{\sqrt3}{2})+++\\\\t<-\frac{\sqrt3}{2}\; \; \; ili\; \; \; t>\frac{\sqrt3}{2}\\\\a)\; \; cos\frac{x}{2}<-\frac{\sqrt3}{2}\\\\\frac{5\pi }{6}+2\pi n<\frac{x}{2}<\frac{7\pi }{6}+2\pi n\; ,\; n\in Z\\\\\frac{5\pi }{3}+4\pi n<x<\frac{7\pi }{3}+4\pi n\\\\b)\; \; cos\frac{x}{2}>\frac{\sqrt3}{2}" align="absmiddle" class="latex-formula">
