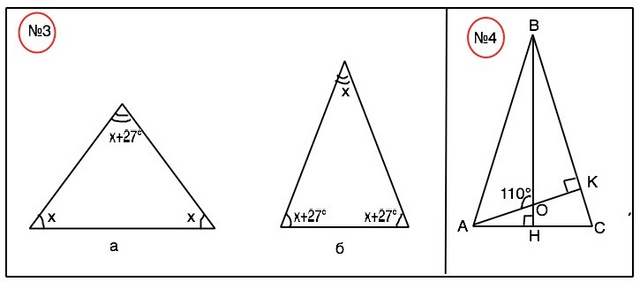
№3. В подобных задачах два варианта решения. а) Больше другого может быть угол при вершине. Примем углы при основании равными х, угол при вершине х+27°. Из суммы углов треугольника 3х+27°=180°, откуда х=51°( углы при основании), 51°+27°=78° ( угол при вершине).
б) Угол при основании больше угла при вершине. Тогда угол при вершине примем равным х, при основании – х+27°. Из суммы углов треугольника 3х=180°- 2•27°=126°, откуда х=42° ( угол при вершине), а углы при основании 42°+27°=69° каждый.
№4. Обозначим высоту из В - ВН, из А - АК, точку пересечения высот О. Тогда в прямоугольном треугольнике АОН по свойству смежных углов угол АОН=180°-110°=70°, а угол ОАН=180°-90°-70°=20°. Треугольник АКС - прямоугольный, угол С=180°-(<К+<А)=<strong>70°. Т.к. ∆ АВС – равнобедренный, углы при основании АС равны по 70°, угол при вершине В=180°-2•70°=40°