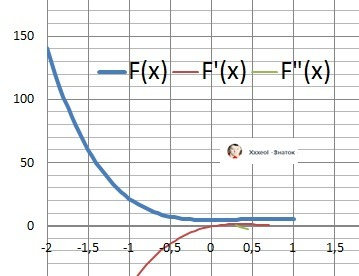
Ответ: Ymin(0) = 5, Ymax(-2) = 141.
Дано:
Y= 3*x⁴ - 8*x³ + 6*x² + 5 - функция.
D(x) = [-2;1] - область определения.
Найти: экстремумы.
Пошаговое объяснение:
Экстремумы в корнях первой производной.
Y'(x) = 12*x³ - 24*x² + 12*x = 12*x*(x-1)² - первая производная.
Корни производной: Х= 0 и Х = 1.
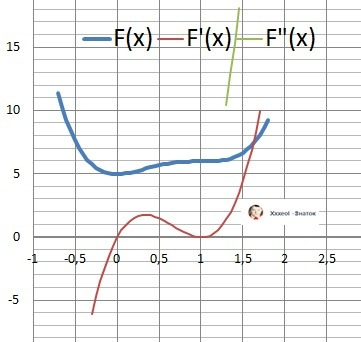
Минимум при Х=0 - Уmin(0) = 5 - ответ.
Думаем: Функция - парабола 4-го порядка - возрастает.
Максимум на границе интервала определения.
Ymax(-2) = 141 - ответ.
На другой границе интервала - Y(1) = 6 - больше минимального.
Рисунки с графиком функции в подарок.