Дано: Y= 2*x² + 8*x+3.
Провести исследование.
1. Описание: Квадратичная парабола,
2. Непрерывная, гладкая. Вертикальных асимптот - нет.
3. Область определения: D(x)=R. X∈(-∞;+∞).
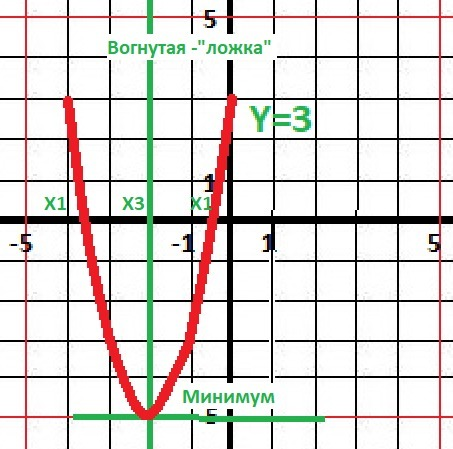
4. Пересечение с осью ОХ -нули функции. Решаем квадратное уравнение. D=40, √40 ≈ 6.325.
X1 = - 3.58, X2 = - 0.42
5. Интервалы знакопостоянства. Парабола положительная, ветви вверх, отрицательна между корней. Непрерывная - квадратные скобки.
Положительна Y>0 при Х∈(-∞;x1]∪[x2;+∞). Y(-∞) = Y(+∞) = + ∞.
Отрицательна Y<0 при Х∈[x1;x2].</p>
6. Пересечение с осью ОУ. Y(0) = 3.
7. Проверка на чётность.
Важно: у чётных функций ВСЕ члены с чётными степенями, у нечётных -ВСЕ с нечётными. Здесь и вторая и первая степени.
Y(-x) ≠ -Y(x). Y(-x)≠ Y(x).
Функция ни чётная ни нечётная.
8. Поиск экстремумов по первой производной.
Y'(x) = 4*x + 8 = 4*(x+2) = 0
x3 = - 2 - одна точка экстремума.
9. Локальный экстремум. Y(x3) = Y(-2) = -5 - минимум.
10. Интервалы монотонности.
Убывает: Х∈(-∞;-2]. Возрастает: Х∈[2;+∞)
11. Поиск точек перегиба по второй производной.
Y"(x) = 4 ≠0. Корней -нет, точек перегиба - нет.
12. Вогнутая - "ложка" во всем D(x). X∈(-∞;+∞)
13. График функции - на рисунке в приложении.