Постройте график функции

$y=\cos^2{(\frac{x}{2}-\frac{\pi}{12})}-\sin^2{(\frac{\pi}{12}-\frac{x}{2})}-1=\\\cos^2{\frac{6x-\pi}{12}}-(-\sin{\frac{6x-\pi}{12}})(-\sin{\frac{6x-\pi}{12}})-1=\\\cos^2{\frac{6x-\pi}{12}}-\sin^2{\frac{6x-\pi}{12}}-1=\\\cos{(2*\frac{6x-\pi}{12})}-1=\cos{(x-\frac{\pi}{6})}-1\\$

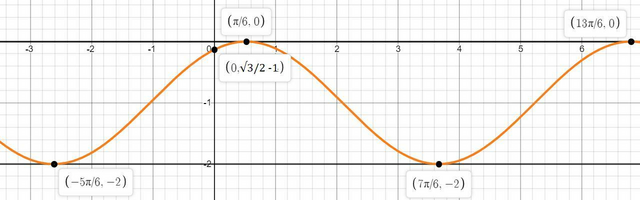
График этой функции будет как у cos x, только он будет опущен на 1 вниз и сдвинут вправо на π/6.

Найдём точки пересечения с осями координат:

$y=\cos{(x-\frac{\pi}{6})}-1=0;x-\frac{\pi}{6}=2\pi n;\\x=\frac{\pi}{6}+2\pi n,n\in \mathbb{Z}.\\y(0)=\cos{(-\frac{\pi}{6})}-1=\frac{\sqrt{3}}{2}-1$

-1 ≤ cos x ≤ 1

Поэтому минимальные и максимальные значения будут в точках с ординатами -2 и 0, т.к. у нас график косинуса, то эти же точки и будут экстремумами.

$\cos{(x-\frac{\pi}{6})}-1=-2;x-\frac{\pi}{6}=-\pi +2\pi n;\\x=-\frac{5\pi}{6}+2\pi n,n\in \mathbb{Z}.$

У нас есть всё чтобы построить график функции.

Смотри вниз.