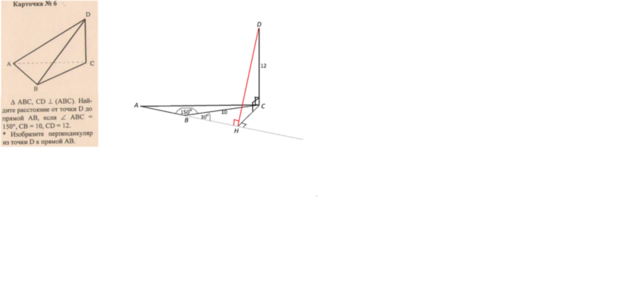
Рисунок к задаче есть, но он не соразмерен условию. Поэтому даю другой.
Расстояние от точки до прямой измеряется отрезком, проведенным из этой точки перпендикулярно прямой.
Вспомним теорему о трех перпендикулярах.
Проекция СН отрезка DH, перпендикулярного АВ, будет также к АВ перпендикулярна.
СН также высота треугольника АВС из вершины С к АВ.
Так как треугольник АВС тупоугольный,
высота СН лежит вне этого треугольника и пересекается с продолжением АВ.
Рассмотрим треугольник ВНС.
Он прямоугольный по построению.
Угол СВН, смежный с углом при вершине В треугольника АВС, равен 30°.
СН противолежит углу 30° и равен половине гипотенузы треугольника ВНС.
СН=5.
Из прямоугольного треугольника DCH уже просто найти DH - расстояние от D до прямой АВ по теореме Пифагора.
Высчитывать не буду, т.к. стороны этого треугольника из Пифагоровых троек (5,12,13). Проверить нетрудно, что расстояние DH равно 13 см