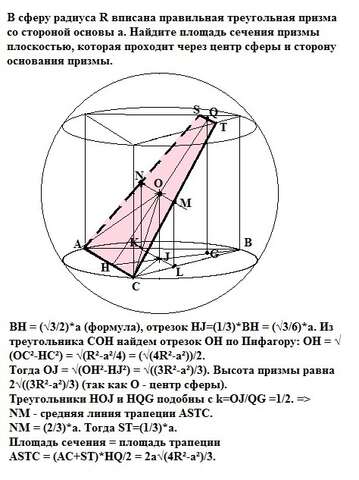
Построение. Проведем высоту основания ВН. В правильном треугольнике это и медиана и биссектриса. Через центр основания J проведем прямую, параллельную стороне АС. Получим точки K и L на пересечении этой прямой с сторонами АВ и ВС соответственно. Через центр сферы О проведем прямую, параллельную стороне АС. Восстановим перпендикуляры из точек К и L и на пересечении этих перпендикуляров с проведенной прямой получим на боковых гранях призмы точки M и N. Проведя через точки А и N, С и М получим линии пересечения секущей плоскости и боковых граней призмы. Сечение призмы - равнобедренная трапеция.
Центр основания призмы J делит высоту основания в отношении 2:1, считая от вершины В (свойство медианы). Высота правильного треугольника ВН = (√3/2)*а (формула), отрезок НJ=(1/3)*ВН = (√3/6)*а. Из треугольника СОН найдем отрезок ОН по Пифагору:
ОН = √(OC²-HC²) = √(R²-a²/4) = (√(4R²-a²))/2.
Тогда OJ = √(OH²-HJ²) = √((3R²-a²)/3). Высота призмы равна
2√((3R²-a²)/3) (так как О - центр сферы).
Треугольники HOJ и HQG подобны с k=OJ/QG =1/2. => NM - средняя линия трапеции ASTC. NM = KL = (2/3)*a (из подобия треугольников АВС и KBL). Тогда ST=(1/3)*a.
Площадь сечения = площадь трапеции ASTC.
Sastc = (AC+ST)*HQ/2 = 2a√(4R²-a²)/3.
Ответ: Sastc = 2a√(4R²-a²)/3.
Для проверки: есть следствие из теоремы об описанной призме: радиус сферы, описанной около правильной треугольной призмы с высотой h и ребром основания a равен R=√(a²/3+h²/4). Подставив найденную высоту призмы, получим R=R.