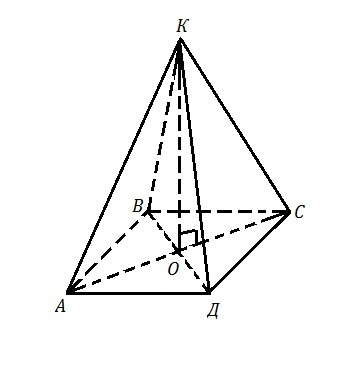
Если точка К равноудалена от вершин квадрата, то она проектируется в центр квадрата (точку пересечения диагоналей, точку О) , КО⊥ пл. АВСД. И длина отрезка КО будет являться расстоянием от точки К до плоскости квадрата АВСД. КО=16 см. Так как КО ⊥ пл. АВСД, то КО перпендикулярен любой прямой в этой плоскости, КО⊥СО.
СО=0,5·АС=0,5·√(АД²+СД²)=0,5·√(144·2+144·2)=0,5·√(2·2·144)=12 см
ΔКОС: ∠КОС=90° , КС=√(КО²+СО²)=√(16²+12²)=20 см