4. По рисунку видно,что треугольник A1BC1 - это часть треугольника ABC по построению.И тогда отсюда следует,что угол B - общий угол и так как прямая(сторона треугольника A1BC1) A1C1 по условию параллельна прямой (стороне треугольника ABC) AC означает,что соответственные углы при жтих двух прямых равны,тогда отсюда следует,что угол BA1C1 = углу BAC(как соответственные углы) и угол BC1A1 = углу BCA(как соответственные углы),что и требовалось доказать.
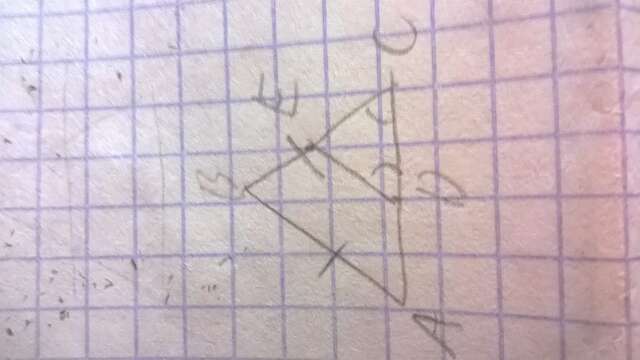
5. Треугольник ABC р/б(равнобедренный),тогда по свойству такого треугольника его углы при основании равны( угол A = углу C). Угол CDE = углу C,а если первый и третий угол равны второму углу,тогда первый и третий углы тоже равны или же короче: угол A = углу CDE,а это соответственные углы при прямых AB и DE,ну, и секущей AD,значит эти прямые параллельны,что и требовалось доказать(ведь 2 прямые параллельны при любой секущей параллельны,если их соответственные углы равны или накрест лежащие углы равны,или сумма односторонних углов равна 180 градусам)