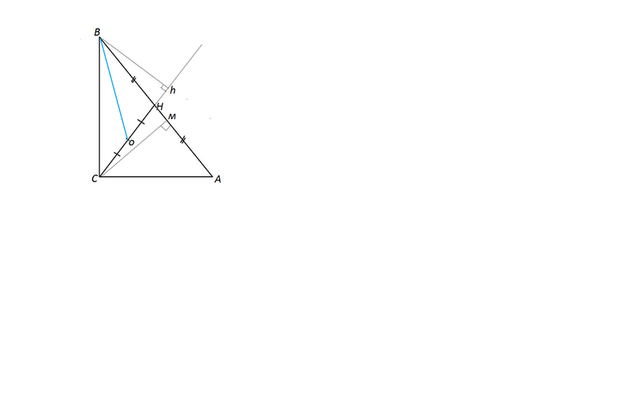
В прямоугольном треугольнике ABC точка О- середина медианы CH, проведенной к гипотенузе AB, AC=6 см, BC=8 см.
Найдите площадь треугольника OBC.
----------Для решения задачи нужно вспомнить, что
медиана делит треугольник на два равновеликих ( т.е. на два треугольника с равной площадью).
В прямоугольном треугольнике медиана СН разделила его на два треугольника.
Высота треугольника СВН и САН одна и та же - СМ, а основания равны.
Следовательно, площадь каждого из этих треугольников равна половине площади треугольника АСВ.
S ACB=АС*ВС
:2=
24 см²
Точно так же медиана ВО треугольника ВСН делит его на два равновеликих треугольника с общей высотой Сh, и площадь каждого равна половине площади треугольника ВСН и, соответственно,
одной четверти площади треугольника АВС.
Площадь треугольника ОВС равна 24:4=6 см²