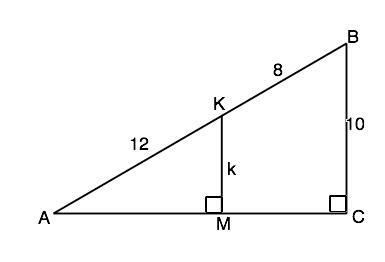
На рис.2 меньший катет прямоугольного треугольника равен 10. Отрезок k перпендикулярен второму катету и делит гипотенузу на отрезки 12 и 8, считая от вершины меньшего острого угла. Найти длину отрезка k
Обозначим треугольник АВС. Гипотенуза АВ, угол С=90°. Отрезок k=KM, АК=12, КВ=8. КМ⊥АС, ВС⊥АС ⇒ ∆ АКМ~∆ АВС по прямому углу и общему острому углу А. Из подобия следует АВ:АК=ВС:КМ, т.е. (12+8):12=10:k, откуда 2k= 12 и k=6.