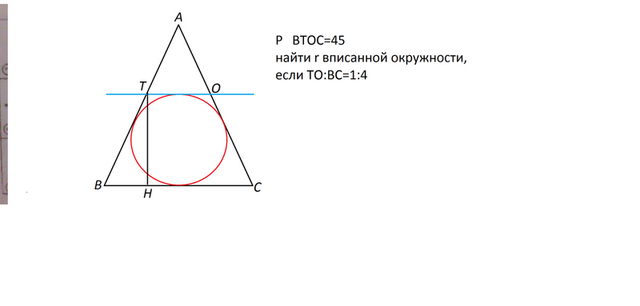
Касательная k, поскольку она параллельна основанию треугольника ВС,
отрезала от него равнобедренную трапецию.
В эту трапецию вписана окружность.
Вспомним, что в трапецию можно вписать окружность тогда и только тогда, когда суммы противоположных сторон трапеции равны.
В получившейся трапеции ВТОС
ТО+ВС=ВТ+ОС
Следовательно,
ТО+ВС=45:2=22,5
Так как отношение ТО:ВС=1:4, частей 1+4=5
ТО=22,5:5=4,5
ВС=4,5*4=18
Опустим из вершины Т высоту ТН
В равнобедренной трапеции высота, опущенная из вершины тупого угла на большее основание, делит его на отрезки, меньший из которых равен полуразности оснований, больший - полусумме оснований.
Отрезок ТН равен полуразности оснований.
ТН=(18-4,5):2= 6,75
ТВ+ОС=45:2=22,5
ТВ=ОС=22,5:2=11,25
Из прямоугольного треугольника ВТН найдем высоту ТН по т. Пифагора.
Она равна √81 ( можете проверить).
ТН=9.
Высота трапеции равна диаметру вписанной окружности.
Радиус r этой окружности равен =9:2=4,5см