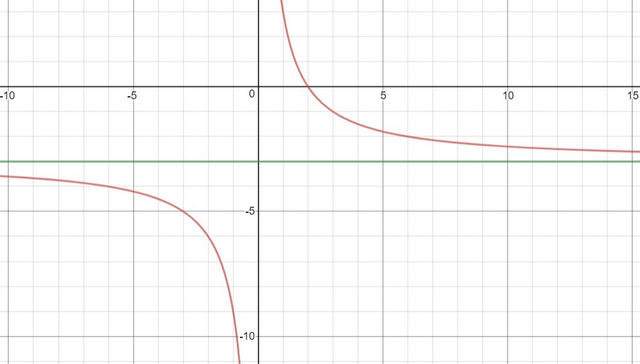
1. Проводим вспомогательную асимптоту, которая параллельна оси х и пересекает ось y в точке -3.
И строим график. См. внизу.
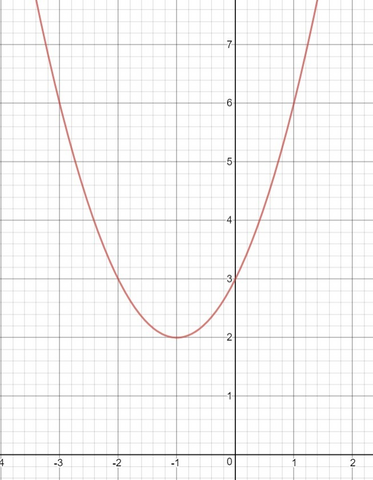
2. 
Имеем параболу, ветви которой вверх, координаты вершины (-1;2).
Пересекает оси:
 net+resheniiy" alt="y(0)=0^2+2*0+3=3;\\x(0): (x+1)^2=-2 => net+resheniiy" align="absmiddle" class="latex-formula">
net+resheniiy" alt="y(0)=0^2+2*0+3=3;\\x(0): (x+1)^2=-2 => net+resheniiy" align="absmiddle" class="latex-formula">
x=-1 --> y=2
x=4 --> y=(4+1)^2+2=27
возрастает: [2;+∞)
не убывает.
Наибольшее значение +∞.
x>0 при y∈(3;+∞)
y>0 при x∈(-∞;+∞)
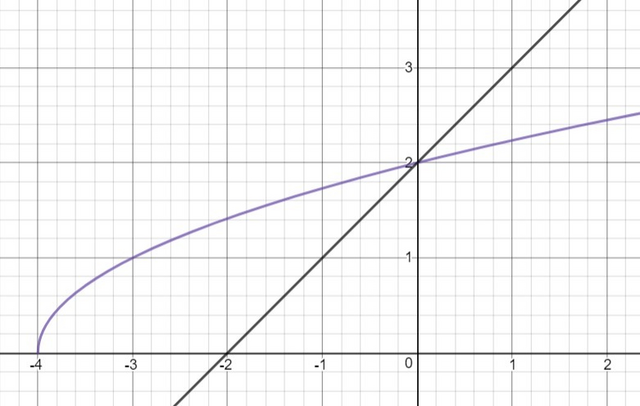
3.
То рисуем корень, который начинается в точке (-4;0)
И прямую, которая составляет с ось х 45° и пересекает ось у в точке 2.